题目内容
8.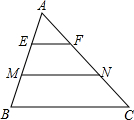 已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.
已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.
分析 由已知条件和平行线得出AM=2AE,AB=3AE,△AEF∽△AMN,△AEF∽△ABC,由相似三角形面积的比等于相似比的平方得出$\frac{△AEF的面积}{△AMN的面积}$=$\frac{1}{4}$,$\frac{△AEF的面积}{△ABC的面积}$=$\frac{1}{9}$,得出$\frac{△AEF的面积}{四边形EMNF的面积}$=$\frac{1}{3}$,$\frac{△AEF的面积}{四边形EBCF的面积}$=$\frac{1}{8}$,即可得出结果.
解答 解:∵E、M是AB边的三等分点,EF∥MN∥BC,
∴AM=2AE,AB=3AE,△AEF∽△AMN,△AEF∽△ABC,
∴$\frac{△AEF的面积}{△AMN的面积}$=($\frac{AE}{AM}$)2=$\frac{1}{4}$,$\frac{△AEF的面积}{△ABC的面积}$=($\frac{AE}{AB}$)2=$\frac{1}{9}$,
∴$\frac{△AEF的面积}{四边形EMNF的面积}$=$\frac{1}{3}$,$\frac{△AEF的面积}{四边形EBCF的面积}$=$\frac{1}{8}$,
∴$\frac{△AEF的面积}{四边形MBCN的面积}$=$\frac{1}{5}$,
∴△AEF的面积:四边形EMNF的面积:四边形MBCN的面积=1:3:5.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
13. 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )| A. | ∠ACB=∠DFE | B. | BE=CF | C. | AB∥DE | D. | AG=CG |
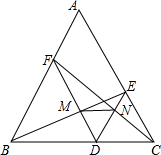 如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形.
如图,在正△ABC中,DE∥AB,DF∥AC,求证:△MDN是等边三角形. 如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.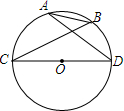 如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.
如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.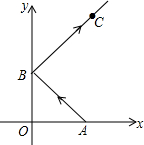 如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2).
如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2). 如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$.
如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$. 如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.