题目内容
14.先化简,再求值:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$,其中x=$\sqrt{2}$,y=$\sqrt{6}$.分析 首先将括号里面进行通分,进而将能分解因式的分解因式,再化简求出答案.
解答 解:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$,
=($\frac{{x}^{2}-y}{x}$-$\frac{{x}^{2}}{x}$-$\frac{x}{x}$)×$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=$\frac{-y-x}{x}$×$\frac{x-y}{x+y}$
=-$\frac{x-y}{x}$,
把x=$\sqrt{2}$,y=$\sqrt{6}$代入得:
原式=-$\frac{\sqrt{2}-\sqrt{6}}{\sqrt{2}}$=-1+$\sqrt{3}$.
点评 此题主要考查了分式的化简求值,正确因式分解是解题关键.

练习册系列答案
相关题目
5.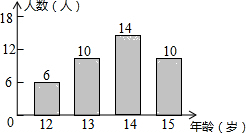 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )| A. | 12岁 | B. | 13岁 | C. | 14岁 | D. | 15岁 |
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
| A. | 108° | B. | 90° | C. | 72° | D. | 60° |
9.下列商标图案中,既不是轴对称图形又不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
 如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )
如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )


