题目内容
1.已知ab≠0,且M=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$,根据a,b,c的不同取值,M有2种不同的值.分析 根据绝对值的意义,可得答案.
解答 解:当a>0,b>0时,M=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$=1+1+1=3;
当a>0,b<0时,M=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$=1-1-1=-1;
当a<0,b>0时,M=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$=-1+1-1=-1,
当a<0,b<0时,M=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$=-1-1+1=-1,
故答案为:2.
点评 本题考查了绝对值,利用负数的绝对值是它的相反数,正数的绝对值是它本身是解题关键,要分类讨论,以防遗漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.一个正方形的边长增加1cm,它的面积就增加了17cm2,这个正方形原来的边长是( )
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
 已知正方形ABCD中,AB=BC=CD=DA=4,∠A=∠B=∠C=∠D=90°.动点P以每秒1个单位速度从点B出发沿线段BC方向运动,动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD-DC-CB方向顺时针作折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.连接PA,当以点Q及正方形的某两个顶点组成的三角形和△PAB全等时,则t为$\frac{4}{5}$,$\frac{4}{3}$,$\frac{8}{5}$,$\frac{12}{5}$.
已知正方形ABCD中,AB=BC=CD=DA=4,∠A=∠B=∠C=∠D=90°.动点P以每秒1个单位速度从点B出发沿线段BC方向运动,动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD-DC-CB方向顺时针作折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.连接PA,当以点Q及正方形的某两个顶点组成的三角形和△PAB全等时,则t为$\frac{4}{5}$,$\frac{4}{3}$,$\frac{8}{5}$,$\frac{12}{5}$.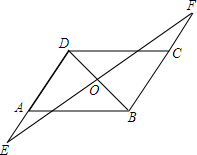 如图,已知AD=BC,AB=CD,O是BD中点,过O作直线交DA的延长线于F,交BC的延长线于F.求证:OE=OF.
如图,已知AD=BC,AB=CD,O是BD中点,过O作直线交DA的延长线于F,交BC的延长线于F.求证:OE=OF.