题目内容
13. 已知正方形ABCD中,AB=BC=CD=DA=4,∠A=∠B=∠C=∠D=90°.动点P以每秒1个单位速度从点B出发沿线段BC方向运动,动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD-DC-CB方向顺时针作折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.连接PA,当以点Q及正方形的某两个顶点组成的三角形和△PAB全等时,则t为$\frac{4}{5}$,$\frac{4}{3}$,$\frac{8}{5}$,$\frac{12}{5}$.
已知正方形ABCD中,AB=BC=CD=DA=4,∠A=∠B=∠C=∠D=90°.动点P以每秒1个单位速度从点B出发沿线段BC方向运动,动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD-DC-CB方向顺时针作折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.连接PA,当以点Q及正方形的某两个顶点组成的三角形和△PAB全等时,则t为$\frac{4}{5}$,$\frac{4}{3}$,$\frac{8}{5}$,$\frac{12}{5}$.
分析 分点Q在AD,DC,CB边上这几种情况进行讨论,根据全等三角形的性质得出对应边相等,进而列出方程求得t的值.
解答 解:当Q在DA上时,如图所示:
此时△APB≌△CQD,
∴BP=DQ,即t=4-4t,
解得t=$\frac{4}{5}$;
当Q在BC边上时,有两个位置,如图所示:
若Q在上边,则△QAD≌△PA,
∴BP=QD,即4t-4=t,
解得t=$\frac{4}{3}$;
若Q在下边,则△APB≌△BQC,
则BP=CQ,即8-4t=t,
解得t=$\frac{8}{5}$;
当Q在AB边上时,如图所示:
此时△APB≌△DQC,
∴BP=CQ,即4t-8=t,解得t=$\frac{8}{3}$,
因为当点P与点Q相遇时停止运动,
所以0≤t≤$\frac{12}{5}$,所以t=$\frac{8}{3}$不合题意;
当P、Q在BC上重合时,△ABP和△ABQ全等,如图所示:
∴此时,t=$\frac{12}{5}$.
故答案为:$\frac{4}{5}$,$\frac{4}{3}$,$\frac{8}{5}$,$\frac{12}{5}$.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质的综合应用,解题时要对点Q的不同位置进行分类讨论,以防漏解,该题综合性较强.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
4.若-1<m<0,且n=$\root{3}{m}$,则m、n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
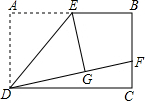 如图,矩形ABCD中,E是AB的中点,将△ADE沿DE折叠后得到GDE,且点G在矩形ABCD的内部,延长DG交BC于点F,若F恰是BC的中点,则$\frac{AB}{AD}$的值是$\sqrt{2}$.
如图,矩形ABCD中,E是AB的中点,将△ADE沿DE折叠后得到GDE,且点G在矩形ABCD的内部,延长DG交BC于点F,若F恰是BC的中点,则$\frac{AB}{AD}$的值是$\sqrt{2}$.