题目内容
9.已知点A(x1,5),B(x2,5)是函数y=(x-1)2+3上两点.则当x=x1+x2时,函数值y=4.分析 由函数解析式可求得其对称轴,再利用对称性可求得x1+x2的值,代入抛物线解析式可求得y值.
解答 解:
∵y=(x-1)2+3,
∴对称轴为x=1,
∵点A(x1,5),B(x2,5)是函数图象上的两点,
∴$\frac{{x}_{1}+{x}_{2}}{2}$=1,
∴x=x1+x2=2,
当x=2时,y=(2-1)2+3=4,
故答案为:4.
点评 本题主要二次函数图象上点的坐标特征,利用对称性求得x1+x2的值是解题的关键.

练习册系列答案
相关题目
4.若-1<m<0,且n=$\root{3}{m}$,则m、n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
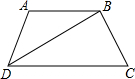 如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.
如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.