题目内容
3．在Rt△ABC中，∠C=90°，AB=41，BC=40，求AC．分析 利用已知直接利用勾股定理求出AC的长．
解答 解：∵Rt△ABC中，∠C=90°，AB=41，BC=40，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{4{1}^{2}-4{0}^{2}}$=9．
点评 此题主要考查了勾股定理，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
11．如果x=2是关于x的方程3-2x=x+a的解，那么a的值应是（ ）
| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
18．将抛物线y=（x-2）2+1向右平移1个单位，再向上平移3个单位后所得抛物线的表达式为（ ）
| A． | y=（x-3）2-2 | B． | y=（x-1）2+4 | C． | y=（x-3）2+4 | D． | y=（x-2）2-2 |
8．平面上有三点，经过每两点作一条直线，则能作出的直线的条数是（ ）
| A． | 1条 | B． | 3条 | C． | 1条或3条 | D． | 以上都不对 |
如图，点E（0，3），O（0，0），C（4，0）在⊙A上，BE是⊙A上的一条弦．则sin∠OBE=$\frac{3}{5}$．
12．
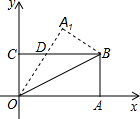如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）
如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）| A． | （$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$） | B． | （$\frac{{\sqrt{3}}}{2}$，$\frac{3}{2}$） | C． | （$\frac{{\sqrt{3}}}{2}$，2） | D． | （$\frac{3}{2}$，$\frac{{\sqrt{3}}}{2}$） |