题目内容
12.计算或解方程:①-12+2×(-3)3+(-6)÷(-$\frac{1}{3}$)2
②18×(-$\frac{2}{3}$)+13×$\frac{2}{3}$-4×$\frac{2}{3}$
③-24-($\frac{1}{4}$-$\frac{1}{6}$-$\frac{1}{12}$)×24
④2(2x+1)=3-2(x-2)
⑤1-$\frac{4y-5}{8}$=$\frac{3-y}{4}$
⑥$\frac{0.3x+0.5}{0.2}$-$\frac{2x-1}{3}$=1.
分析 ①原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
②原式逆用乘法分配律计算即可得到结果;
③原式利用乘方的意义,以及乘法分配律计算即可得到结果;
④方程去括号,移项合并,把x系数化为1,即可求出解;
⑤方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
⑥方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:①原式=-1-54-54=-109;
②原式=$\frac{2}{3}$×(-18+13-4)=$\frac{2}{3}$×(-9)=-6;
③原式=-16-6+4+2=-16;
④去括号得:4x+2=3-2x+4,
移项合并得:6x=5,
解得:x=$\frac{5}{6}$;
⑤去分母得:8-4y+5=6-2y,
移项合并得:-2y=-7,
解得:y=$\frac{7}{2}$;
⑥方程整理得:$\frac{3x+5}{2}$-$\frac{2x-1}{3}$=1,
去分母得:9x+15-4x+2=6,
移项合并得:5x=-11,
解得:x=-2.2.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
20.已知点M到x轴、y轴的距离分别为4和6,且点M在x轴的上方、y轴的左侧,则点M的坐标为( )
| A. | (4,-6) | B. | (-4,6) | C. | (6,-4) | D. | (-6,4) |
7.抛物线y=x2-2x+3 的对称轴为( )
| A. | 直线x=-1 | B. | 直线x=-2 | C. | 直线x=1 | D. | 直线x=2 |
17.在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B,则下列条件:
①AC=A′C′;②BC=B′C′;③∠B=∠B′;④∠C=∠C′中能够判定△ABC≌△A′B′C′的有( )
①AC=A′C′;②BC=B′C′;③∠B=∠B′;④∠C=∠C′中能够判定△ABC≌△A′B′C′的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列方程不是一元二次方程的是( )
| A. | $\sqrt{3}{x^2}+2x+1=0$ | B. | 0.1x2-0.5x+1.8=0 | ||
| C. | $\frac{1}{2}{x^2}=1-\frac{3}{5}x$ | D. | x2+x-1=(x+1)2 |
1.在函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x≥2 | B. | x≥-2 | C. | x>2 | D. | x>-2 |
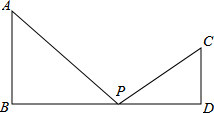 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.