题目内容
10.若a,b为有理数,且$\sqrt{8}$+$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,则ab=0.分析 先把等式左边化简得到$\frac{21\sqrt{2}}{4}$=a+b$\sqrt{2}$,由a,b为有理数,则得到a=0,b=$\frac{21}{4}$,即可计算ab=0.
解答 解:∵$\sqrt{8}$+$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=2$\sqrt{2}$+3$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=$\frac{21\sqrt{2}}{4}$,
∴$\frac{21\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴a=0,b=$\frac{21}{4}$,
∴ab=0,
故答案为0.
点评 本题考查了二次根式的加减法:先把二次根式化为最简二次根式,然后合并同类二次根式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,如果这样卖出去,那么商店( )
| A. | 不盈不亏 | B. | 盈利50元 | C. | 盈利8元 | D. | 亏损8元 |
1.某商场卖出两部进价不同的手机,都卖了1200元,其中一部盈利20%,另一部亏损20%,在这次买卖中,这家商场( )
| A. | 赔了100元 | B. | 赚了100元 | C. | 不赔不赚 | D. | 赚了180元 |
19.①若(t-3)2-2t=1,则t=2或4;②已知2a=5b=10,则a+b=ab.( )
| A. | ①对,②错 | B. | ①错,②对 | C. | ①②都错 | D. | ①②都对 |
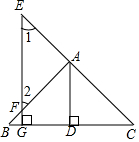 如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.
如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.