题目内容
5.有三张正面分别标有数字-2,0,1的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽取一张,将该卡片的数字记为a:放回后洗匀.再从中抽取一张,将该卡片上的数字记为b,则使得函数y=(a+2)x2-bx$+\frac{1}{4}a$的图象与x轴有交点的概率为$\frac{5}{9}$.分析 画树状图列出所有等可能结果,再根据判别式得出a、b需满足的条件,从而得到满足条件的结果数,由概率公式可得答案.
解答 解:画树状图如下:
∵函数y=(a+2)x2-bx$+\frac{1}{4}a$的图象与x轴有交点,
∴△=b2-4×(a+2)×$\frac{1}{4}$=b2-a-2≥0,
满足以上条件的有a=-2,b=-2、0、1或a=0,b=-2或a=1,b=-2这5种结果,
∴使得函数y=(a+2)x2-bx$+\frac{1}{4}a$的图象与x轴有交点的概率为$\frac{5}{9}$,
故答案为:$\frac{5}{9}$.
点评 考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到使函数图象与x轴有交点的情况数是解决本题的关键.

练习册系列答案
相关题目
15. 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )| A. | 50人中必有2人的生日相同 | B. | 100人中必有2人的生日相同 | ||
| C. | 365人中必有2人的生日相同 | D. | 367人中必有2人的生日相同 |
16.如图,根据根据图中提供的信息,可知一个杯子的价格是( )


| A. | 51元 | B. | 35元 | C. | 8元 | D. | 7.5元 |

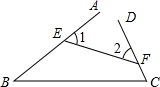 如图,点E、F分别在AB、CD上,若∠B=40°,∠C=70°,则∠1+∠2=110°.
如图,点E、F分别在AB、CD上,若∠B=40°,∠C=70°,则∠1+∠2=110°.