题目内容
已知a≠b且
-
=0.求证:
+
=
.
| a2 |
| ab+b2 |
| b2 |
| a2+ab |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a+b |
考点:分式的混合运算
专题:证明题
分析:由已知条件得到a4+a3b-ab3-b4=0,再利用因式分解得到∴(a2-b2)(a2+b2+ab)=0,而a≠b,则a2+b2+ab=0,根据完全平方公式得到(a+b)2=ab,再利用等式的性质变形即可得到
+
=
.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a+b |
解答:证明:∵
-
=0,
∴a4+a3b-ab3-b4=0,
∴(a2+b2)(a2-b2)+ab(a2-b2)=0,
∴(a2-b2)(a2+b2+ab)=0,
而a≠b,
∴a2+b2+ab=0,
∴a2+b2+2ab=ab,
∴(a+b)2=ab
∴
=1,
∴
=
,
∴
+
=
.
| a2 |
| ab+b2 |
| b2 |
| a2+ab |
∴a4+a3b-ab3-b4=0,
∴(a2+b2)(a2-b2)+ab(a2-b2)=0,
∴(a2-b2)(a2+b2+ab)=0,
而a≠b,
∴a2+b2+ab=0,
∴a2+b2+2ab=ab,
∴(a+b)2=ab
∴
| (a+b)2 |
| ab |
∴
| a+b |
| ab |
| 1 |
| a+b |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a+b |
点评:本题考查了分式的混合运算:分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
下列方程是一元二次方程的是( )
| A、x2+y2=0 | ||||
| B、y2=2x-1 | ||||
| C、(x+1)2=2(x+1) | ||||
D、
|
已知反比例函数y=
,下列结论中正确的是( )
| 2 |
| x |
| A、无论x取何值时,y随x的增大而增大 |
| B、当x<0时,图象在第二象限 |
| C、图象不是轴对称图形 |
| D、图象经过点(-1,-2) |
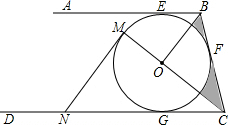 如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N. 如图,在梯形ABCD中,AD∥BC,E和F分别是BD,AC的中点,若BC=10,AD=6,则线段EF的长为( )
如图,在梯形ABCD中,AD∥BC,E和F分别是BD,AC的中点,若BC=10,AD=6,则线段EF的长为( )