题目内容
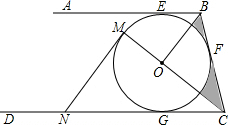 如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别于⊙O相切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.(1)求证:MN是⊙O的切线;
(2)当0B=6cm,OC=8cm时,求⊙O的半径及图中阴影部分的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)求证MN是⊙O的切线,可以通过证明∠NMC=90°得出;
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,图中阴影部分的面积=△OBC的面积-扇形的面积.
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,图中阴影部分的面积=△OBC的面积-扇形的面积.
解答: (1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
∴∠OBC=
∠ABC,∠DCB=2∠DCM.
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=
(∠ABC+∠DCB)=
×180°=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°.
∵MN∥OB,
∴∠NMC=∠BOC=90°,即MN⊥MC 且MO是⊙O的半径,
∴MN是⊙O的切线;
(2)解:连接OF,则OF⊥BC.
由(1)知,△BOC是直角三角形,
∴BC=
=
=10,
∵S△BOC=
•OB•OC=
•BC•OF,
∴6×8=10×OF,
∴0F=4.8cm,
∴⊙O的半径为4.8cm.
∴S阴影=
×6×8-
=24-5.76π(cm2).
综上所述,⊙O的半径是4.8cm,图中阴影部分的面积是(24-5.76π)cm2.
 (1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,∴∠OBC=
| 1 |
| 2 |
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°.
∵MN∥OB,
∴∠NMC=∠BOC=90°,即MN⊥MC 且MO是⊙O的半径,
∴MN是⊙O的切线;
(2)解:连接OF,则OF⊥BC.
由(1)知,△BOC是直角三角形,
∴BC=
| OB2+OC2 |
| 62+82 |
∵S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴6×8=10×OF,
∴0F=4.8cm,
∴⊙O的半径为4.8cm.
∴S阴影=
| 1 |
| 2 |
| 90π×4.82 |
| 360 |
综上所述,⊙O的半径是4.8cm,图中阴影部分的面积是(24-5.76π)cm2.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?若设每轮传染中平均一个人传染了x个人,那么x满足的方程是( )
| A、x(1+x)=121 |
| B、1+x(1+x)=121 |
| C、x+x(1+x)=121 |
| D、1+x+x(1+x)=121 |
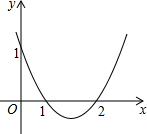 如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2=
如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2= 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.
如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.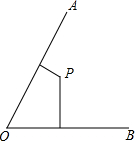 已知∠AOB=60°,P为角内部一点,P到OA、OB的距离分别为1和5,在射线OA上找一点M,在射线OB上找一点N,使PM+PN最小,则最小值为
已知∠AOB=60°,P为角内部一点,P到OA、OB的距离分别为1和5,在射线OA上找一点M,在射线OB上找一点N,使PM+PN最小,则最小值为