题目内容
等腰梯形两底之差为6，腰为6，则梯形较小的底角是 ．
考点：等腰梯形的性质
专题：
分析：如图，等腰梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB，过A点作AE∥CD，平移一腰，把问题转化到△ABE中，判断三角形的形状，然后根据三角形ABE的形状来计算该梯形的较小底角∠B的度数即可．
解答：解：如图，过A点作AE∥CD，交BC于E点，则AECD为平行四边形，
则AE=CD=AB=6，
∵梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB=6，
∴AB=BC-AD=BC-CE=BE，
又∵AB=CD，
∴AB=BE=AE，
∴△ABE为等边三角形，
∴∠B=60°．
故答案为：60°．
则AE=CD=AB=6，
∵梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB=6，
∴AB=BC-AD=BC-CE=BE，
又∵AB=CD，
∴AB=BE=AE，
∴△ABE为等边三角形，
∴∠B=60°．
故答案为：60°．
点评：本题考查了等腰梯形的性质的应用，注意：平移一腰，能将两腰、两底差，两底角集中在一个三角形中，形成特色三角形．
练习册系列答案
相关题目
一个函数的图象是双曲线（如图），根据图象，求出这个函数的解析式和m的值．
如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G，求证：AC•DG=AG•DF．
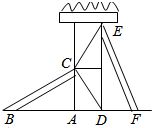如图，有两个长度相等的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等，若∠ABC=32°，则∠DFE的度数为（ ）| A、32° | B、28° |
| C、58° | D、45° |
如图所示，被遮挡的点的坐标可能是（ ）| A、（-2，-3） |
| B、（-2，3） |
| C、（2，-3） |
| D、（2，3） |
计算
-
的结果是（ ）
| 2 |
| x-2 |
| x |
| x-2 |
| A、0 | B、1 | C、-1 | D、2 |