题目内容
19. 利用“等边对等角”
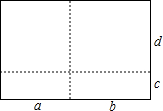
利用“等边对等角”如图,AB=AD,CD∥AB,CE∥AD.
求证:△CDE是等腰三角形.
分析 由AB=AD推出∠ADB=∠B,再根据平行线性质可以证明∠CED=∠CDE由此即可证明.
解答 证明: ∵AB=AD,
∵AB=AD,
∴∠ADB=∠B,
∵CD∥AB,
∴∠CDE=∠B,
∵CE∥AD,
∴∠CED=∠ADB,
∴∠CED=∠CDE,
∴CE=CD,
∴△CDE是等腰三角形.
点评 本题考查平行线的性质、等腰三角形的判定等知识,解题的关键是熟练掌握这些知识,学会转化的思想,欲证明边相等可以转化为证明角相等,属于中考常考题型.

练习册系列答案
相关题目
17.下列各式:$\frac{1}{8}(1-x)$,$\frac{4x}{π-3}$,$\frac{{{x^2}-{y^2}}}{2}$,$\frac{1}{x}+x$,$\frac{{5{x^2}}}{x}$,其中分式共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.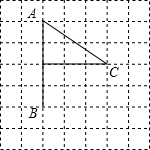 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
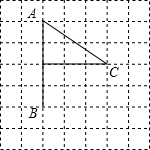 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
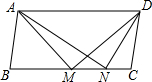 如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)
如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)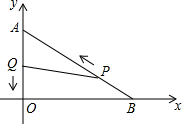 如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).
如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).