题目内容
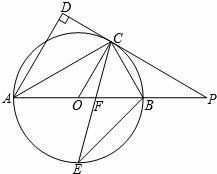
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,与边AC交于点E,过点D作DF⊥AC于F.
(1)求证:DF为⊙O的切线;
(2)若DE= ,AB=
,AB=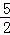 ,求AE的长.
,求AE的长.
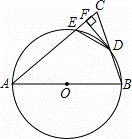
(1)证明:连接AD,OD;
∵AB为⊙O的直径,
∴∠ADB=90°,
即AD⊥BC;
∵AB=AC,
∴BD=DC.
∵OA=OB,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD.
∴∠ODF=∠DFA=90°,
∴DF为⊙O的切线.
(2)解:连接BE交OD于G;
∵AC=AB,AD⊥BC,ED=BD,
∴∠EAD=∠BAD.
∴ .
.
∴ED=BD,OE=OB.
∴OD垂直平分EB.
∴EG=BG.
又AO=BO,
∴OG= AE.
AE.
在Rt△DGB和Rt△OGB中,
BD2﹣DG2=BO2﹣OG2
∴( )2﹣(
)2﹣( ﹣
﹣ OG)2=BO2﹣OG2
OG)2=BO2﹣OG2
解得:OG= .
.
∴AE=2OG= .
.


练习册系列答案
相关题目


 B.3
B.3 C.
C.

 .
. ,求tan∠DBC的值.
,求tan∠DBC的值.

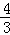 ,BE=7
,BE=7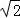 ,求线段PC的长.
,求线段PC的长.