题目内容
如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD .
.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC= ,求tan∠DBC的值.
,求tan∠DBC的值.

(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠AEO=∠ACB=90°,
∴OD⊥AC,
∴ =
= ,
,
∴AD=CD;
(2)解:∵AB=10,
∴OA=OD= AB=5,
AB=5,
∵OD∥BC,
∴∠AOE=∠ABC,
在Rt△AEO中 ,
,
OE=OA•cos∠AOE=OA•cos∠ABC=5× =3,
=3,
∴DE=OD﹣OE=5﹣3=2,
∴AE= =
= =4,
=4,
在Rt△AED中, tan∠DAE= =
= =
= ,
,
∵∠DBC=∠DAE,
∴tan∠DBC= .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 1B1C1,点C1的坐标是 ;
1B1C1,点C1的坐标是 ;
 ,AB=
,AB=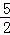 ,求AE的长.
,求AE的长.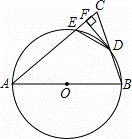
 B.
B. C.
C.  D.
D. 

 ,则BC的长是( )
,则BC的长是( )
 D. 4
D. 4 ≈1.414,
≈1.414, ≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).
≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).