题目内容
解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.
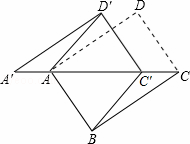
(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A′C′的位置时,A′C′的长为 m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).

解:(I)∵点C是AB的中点,
∴A'C'= AB=23.5m.
AB=23.5m.
(II)设PQ=x,
在Rt△PMQ中,tan∠PMQ= =1.4,
=1.4,
∴MQ=
 ,
,
在Rt△PNQ中,tan∠PNQ= =3.3,
=3.3,
∴NQ= ,
,
∵MN=MQ﹣NQ=40,即 ﹣
﹣ =40,
=40,
解得:x≈97.
答:解放桥的全长约为97m.

练习册系列答案
相关题目
 ,AB=
,AB=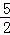 ,求AE的长.
,求AE的长.

 B.
B. C.
C. D.
D. 

 ≈1.414,
≈1.414, ≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).
≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).