题目内容
20．一直角三角形两直角边的和是6cm，其中一边长xcm．（1）设这个三角形面积为S，求S的最大值．
（2）设以这个直角的三角形的斜边长为边长的正方形的面积为S正，求S正的最小值．
分析 （1）根据直角三角形的一直角边为x，则另一直角边长为6-x，根据三角形的面积公式即可得出结论；
（2）设一直角边长为x，表示出另一直角边，再利用勾股定理列式表示出斜边的平方，即为正方形的面积，然后整理出顶点式形式，再利用二次函数的最值问题求解．
解答 解：（1）∵直角三角形的两条直角边之和是6，
∴直角三角形的一直角边为x，斜边长为y，则另一直角边长为6-x，
∴S=x（6-x），即S=-x2+6x，
∴S最大=$\frac{-{6}^{2}}{4×（-1）}$=9；
（2）设斜边长为y，直角三角形的一直角边为x，则另一直角边长为6-x，
由勾股定理得：y2=x2+（6-x）2=2x2-12x+36，
∴设以这个直角的三角形的斜边长为边长的正方形的面积S正=y2，
即S正=2x2-12x+36=2（x-3）2+18，
所以，当x=3时，即三角形为等腰直角三角形时，以此三角形的斜边为边长的正方形面积有最小值为18．
点评 本题考查了二次函数的最值问题，勾股定理，此类题目，整理出顶点式形式求解更简便．
练习册系列答案
阅读快车系列答案
相关题目
如图所示是由几个小立方块所搭的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请画出相应几何体的主视图和左视图．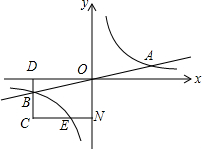
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点．过点B作矩形DCNO交x轴于点D．交Y轴于点N．交双曲线y=$\frac{k}{x}$于点E．若B是CD的中点，四边形OBCE的面积为4，则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$．
如图，用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体，这个多面体共有12条棱．
10．下列说法其中正确的有（ ）
（1）最小的正整数是1，最大的负整数是-1；
（2）相反数等于它本身的数只有0，倒数等于它本身的数是±1
（3）绝对值等于它本身的数是非负数，绝对值等于它的相反数的数是非正数
（4）绝对值相等的两个数一定相等，绝对值不相等的两个数一定不相等．
（1）最小的正整数是1，最大的负整数是-1；
（2）相反数等于它本身的数只有0，倒数等于它本身的数是±1
（3）绝对值等于它本身的数是非负数，绝对值等于它的相反数的数是非正数
（4）绝对值相等的两个数一定相等，绝对值不相等的两个数一定不相等．
| A． | （1），（2），（3） | B． | （2），（3），（4） | C． | （1），（3），（4） | D． | （1），（2），（3），（4） |