题目内容
14.解不等式:|2x+1|>|x-2|分析 根据x值的不同分情况进行绝对值的化简,然后解不等式.
解答 解:当x<-$\frac{1}{2}$时,不等式可化为:
-2x-1>2-x,
解得:x<-3,
x<-3;
当-$\frac{1}{2}$≤x≤2时,不等式可化为:
2x+1>2-x,
解得:x>$\frac{1}{3}$,
∴$\frac{1}{3}$<x≤2;
当x>2时,不等式可化为:
2x+1>x-2,
解得:x>-3,
∴x>2.
综上所述,不等式的解集为x<-3或x>$\frac{1}{3}$.
点评 本题考查了不等式的解法和绝对值的化简,解答本题的关键是根据x值的不同分情况进行绝对值的化简.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.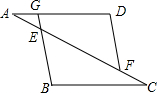 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )| A. | $\frac{AG}{AD}=\frac{AE}{AF}$ | B. | $\frac{AG}{AD}=\frac{EG}{DF}$ | C. | $\frac{AE}{AC}=\frac{AG}{AD}$ | D. | $\frac{AD}{BC}=\frac{DF}{BE}$ |
5.为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如表中是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元,请问表中二档电价、三档电价各是多少?
| 阶梯 | 电量 | 电价 |
| 一档 | 0-180度 | 0.6元/度 |
| 二档 | 181-400度 | 二档电价 |
| 三档 | 401度及以上 | 三档电价 |
2.下列各式运算正确的是( )
| A. | a3+a2=2a5 | B. | a3-a2=a | C. | (a3)2=a5 | D. | a6÷a3=a3 |
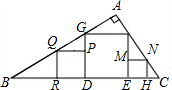 如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系.
如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系.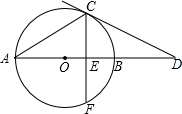 如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.