题目内容
15.①阅读下面内容:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}-2$.
②计算:
(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$;
(2)$\frac{4}{\sqrt{13}-3}$;
(3)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数).
分析 一般二次根式的有理化因式是符合平方差公式的特点的式子.据此作答.
解答 解:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$;
(2)$\frac{4}{\sqrt{13}-3}$=$\frac{4×(\sqrt{13}+3)}{(\sqrt{13}-3)(\sqrt{13}+3)}$=$\sqrt{13}$+3;
(3)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}-\sqrt{n}$(n为正整数).
点评 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.不改变原式的值,将式子12-(+3)-(-4)+(-6)中的减法改成加法并省略括号、加号,则正确的结果是( )
| A. | -12-3+4-6 | B. | 12-3-4-6 | C. | 12-3+4-6 | D. | 12+3-4-6 |
 如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )
如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )



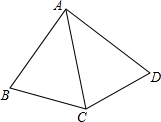 如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.