题目内容
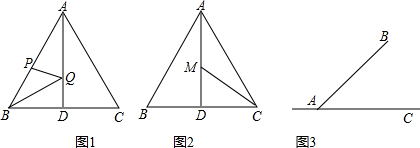
7. 如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )
如图,△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=6cm,动点P从点B出发,以1cm/s的速度,沿B→A的方向运动,到达点A时停止,动点Q从点A出发,以2cm/s的速度,沿A→C的方向运动,到达点C时停止,P、Q两点同时出发,设运动的时间为t(s),△APQ的面积为S(cm2),则S关于t的函数图象大致为( )| A. |  | B. |  | C. |  | D. |  |
分析 过点P作PE⊥AC与点E,得到△PAE~△PBD,求出PE=-$\frac{3}{5}$t+6,分类讨论:当0≤t≤5时;当5<t≤10时,分别求出函数解析式,即可解答.
解答 解:过点P作PE⊥AC与点E,
则BP=t,AP=10-t,AQ=2t,
∵BD⊥AC,PE⊥AC,
∴△PAE~△PBD,
∴$\frac{PE}{BD}=\frac{AP}{AB}$,
∴$\frac{PE}{6}=\frac{10-t}{10}$,
∴PE=-$\frac{3}{5}$t+6,
当0≤t≤5时,S=$\frac{1}{2}$AQ•PE=$\frac{1}{2}•2t•(-\frac{3}{5}t+6)$=$-\frac{3}{5}{t}^{2}$+6t.图象为二次函数,开口向下;
当5<t≤10时,点Q运动到点C停止不动,S=$\frac{1}{2}$AQ•PE=$\frac{1}{2}$×10•(-$\frac{3}{5}$t+6)=-3t+30,图象为一次函数,
故选:D.
点评 本题考查了动点函数的图象问题,解决本题的关键是进行分类讨论.

练习册系列答案
相关题目