题目内容
5.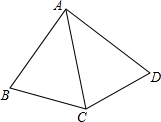 如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
如图,在四边形ABCD中,AC平分∠BAD,AC2=AB•AD.试说明∠BCD=∠B+∠D的理由.
分析 根据角平分线的定义得到∠CAD=∠CAB,由AB2=AC•AD,得到AC:AB=AD:AC,证得△ABC∽△ACD,根据相似三角形的性质得到∠ACD=∠B,∠ACB=∠D,等量代换即可得到结论.
解答 证明:∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵AB2=AC•AD,
∴AC:AB=AD:AC,
∴△ABC∽△ACD,
∴∠ACD=∠B,∠ACB=∠D,
∵∠BCD=∠ACD+∠ACB,
∴∠BCD=∠B+∠D.
点评 本题考查了相似三角形的判定和性质,角平分线的性质,三角形外角的性质,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
14.课本上用直尺和圆规作一个角的平分线,其中三角形全等的依据是( )
| A. | AAS | B. | SSS | C. | SAS | D. | ASA |
15.为了比较甲、乙两名射击运动员的射击成绩谁更稳定,每人各射击10次,并对这10次成绩(环)进行统计,如果两人的平均成绩相等,甲、乙的方差分别是0.3、0.5,则下列说法正确的是( )
| A. | 甲的射击成绩更稳定 | B. | 乙的射击成绩更稳定 | ||
| C. | 甲、乙的射击成绩一样稳定 | D. | 无法确定甲、乙射击成绩谁更稳定 |
 如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.
如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.