题目内容
20.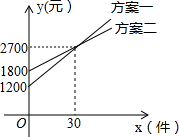 某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.
某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.
分析 先计算方案一和方案二的函数解析式,列出相应的方案二增加报酬后的解析式,根据销售产品达到40件时,两种方案的报酬差额不超过100元,列不等式组解出即可.
解答 解:设方案一的函数解析式为:y1=kx+b,
把(0,1200),(30,2700)代入得:$\left\{\begin{array}{l}{b=1200}\\{30k+b=2700}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=1200}\\{k=500}\end{array}\right.$,
∴y1=50x+1200,
同理得:方案二的函数解析式为:y2=30x+1800,
增加报酬后方案二的解析式为:y2=(30+m)x+1800,
当x=40时,根据题意得:
①50x+1200-[(30+m)x+1800]≤100,
m≥2.5;
②[(30+m)x+1800-50x-1200]≤100,
m≤7.5;
∴2.5≤m≤7.5;
故答案为:2.5≤m≤7.5.
点评 本题是一次函数的应用,主要考查了用待定系数法求一次函数的解析式,与不等式组相结合,在解题过程中应注意数形结合,使求解过程变得简单.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
8.某校初一数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
根据表格提供的信息,下列说法错误的是( )
| 支撑物高度h/cm | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 小车下滑时间t/s | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 |
| A. | 支撑物的高度为40cm,小车下滑时间为2.13s | |
| B. | 支撑物高度h越大,小车下滑时间t越小 | |
| C. | 若小车下滑时间为2s,则支撑物高度在40cm至50cm之间 | |
| D. | 若支撑物的高度为80cm,则小车下滑时间可以使小于1.59s的任意值 |
12.把一张矩形的纸片对折后和原矩形相似,那么大矩形与小矩形的相似比是( )
| A. | $\sqrt{2}$:1 | B. | 4:1 | C. | 3:1 | D. | 2:1 |
9.下列三角形中,能全等的是( )
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
| A. | (1)(3) | B. | (2)(4) | C. | (1)(4) | D. | (1)(3)(4) |
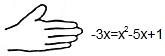 老师在黑板上写了一个正确的计算过程,随后用手捂住了一个二次三项式,形式如下:
老师在黑板上写了一个正确的计算过程,随后用手捂住了一个二次三项式,形式如下: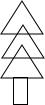 如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.
如图,小王用纸片做了一棵圣诞树放在桌子上,这棵树由三张同大小的正三角形纸片和一张正方形纸片组成,已知圣诞树共遮住了81cm2的面积,其中长形的面积是12cm2(长方形与三角形接缝处的面积忽略不计)三角形纸片的重叠部分分为两个相同大小、面积均为xcm2的小正三角形,且大正三角形的面积比小正三角形的面积的8倍还大1cm2,求一个大正三角形的面积.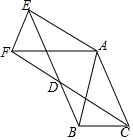 △ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,