题目内容
2. 如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.
如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.
分析 根据角平分线的定义可得∠AOD=2∠AOC,再根据邻补角的定义表示出∠BOD,再表示出∠AOC,然后根据互为余角的两个角的和等于90°表示出∠BOD的余角,最后列方程求解得到∠即可.
解答 解:∵OC是∠AOD的平分线,
∴∠AOD=2∠AOC,
∴∠BOD=180°-∠AOD=180°-2∠AOC,
∴∠AOC=90°-$\frac{1}{2}$∠BOD,
由题意得,90°-∠BOD=$\frac{1}{3}$(90°-$\frac{1}{2}$∠BOD),
解得∠BOD=72°,
所以,∠BOD的邻补角=180°-∠BOD=180°-72°=108°.
点评 本题考查了余角和补角,对顶角、邻补角的定义,角平分线的定义,熟记概念与性质并准确识图是解题的关键.

练习册系列答案
相关题目
 如图,点O为直线AB上一点,过点O作射线OC,已知0°<∠AOC<90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.
如图,点O为直线AB上一点,过点O作射线OC,已知0°<∠AOC<90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE. 如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.
如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.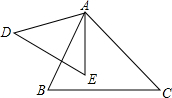 如图所示,在△ABC与△ADE中,AB•ED=AE•BC,要使△ABC与△ADE相似,还需要添加一个条件,这个条件是∠B=∠E(答案不唯一)(只加一个即可)并证明.
如图所示,在△ABC与△ADE中,AB•ED=AE•BC,要使△ABC与△ADE相似,还需要添加一个条件,这个条件是∠B=∠E(答案不唯一)(只加一个即可)并证明.