题目内容
10. 如图,点O为直线AB上一点,过点O作射线OC,已知0°<∠AOC<90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.
如图,点O为直线AB上一点,过点O作射线OC,已知0°<∠AOC<90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.(1)求∠DOE的度数;
(2)求∠FOB+∠DOC的度数.
分析 (1)根据射线OD平分∠AOC,射线OE平分∠BOC,判断出∠AOD=∠COD=$\frac{1}{2}$∠AOC,∠COE=∠BOE=$\frac{1}{2}$∠BOC,即可求出∠DOE的度数是多少即可.
(2)根据射线OF平分∠DOE,可得∠DOF=∠EOF=$\frac{1}{2}$∠DOE=45°,据此求出∠FOB+∠DOC的度数是多少即可.
解答 解:(1)∵射线OD平分∠AOC,
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC;
∵射线OE平分∠BOC,
∴∠COE=∠BOE=$\frac{1}{2}$∠BOC;
∵∠AOC+∠BOC=180°,
∴∠DOE=∠DOC+∠EOC
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC
=$\frac{1}{2}$(∠AOC+∠BOC)
=$\frac{1}{2}$×180°
=90°
(2)∵射线OF平分∠DOE,
∴∠DOF=∠EOF=$\frac{1}{2}$∠DOE=45°,
∴∠FOB+∠DOC
=∠BOF+∠AOD
=180°-∠DOF
=180°-45°
=135°
点评 此题主要考查了角的计算,以及角的平分线的性质和应用,要熟练掌握.

练习册系列答案
相关题目
 如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(-4,0),B(-1,1),C(-2,3).
如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(-4,0),B(-1,1),C(-2,3).  如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.
如图,点O是直线AB上的一点,OC是∠AOD的平分线,已知∠BOD的余角等于∠AOC的$\frac{1}{3}$,求∠BOD的邻补角的度数.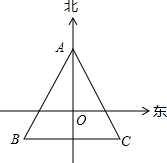 如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置.
如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置.