题目内容
 快、慢两车分别从相距360千米的甲乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后安原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)之间的关系如图,请结合图象信息解答下列问题:
快、慢两车分别从相距360千米的甲乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后安原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)之间的关系如图,请结合图象信息解答下列问题:(1)两车匀速行驶的速度各是多少?
(2)求线段BD的解析式.
(3)出发多少小时,快、慢两车距各自出发地的距离相等?
考点:一次函数的应用
专题:
分析:(1)根据图中数据得出两车行驶的距离与行驶时间的关系进而得出两车的速度;
(2)根据两车的速度得出B,D,E点坐标,进而得出设BD和OE直线解析式;
(3)由(2)得出交点坐标横坐标即可得出答案.
(2)根据两车的速度得出B,D,E点坐标,进而得出设BD和OE直线解析式;
(3)由(2)得出交点坐标横坐标即可得出答案.
解答:解;(1)如图所示:快车一共行驶了7小时,中间停留了1小时,慢车一共行驶了6小时,
∵由图可得出两地相距360km,
∴快车速度为:360×2÷6=120(km/h),
慢车速度为:360÷6=60(km/h);
(2)∵快车速度为:120km/h,
∴360÷120=3(h),
∴A点坐标为;(3,360)
∴B点坐标为(4,360),
可得E点坐标为:(6,360),D点坐标为:(7,0),
∴设BD解析式为:y=kx+b,
,
解得:
.
∴BD解析式为:y=-120x+840,
设OE解析式为:y=ax,
∴360=6a,
解得:a=60,
∴OE解析式为:y=60x;
(3)当0<x<3时,
快车距出发地的距离为120x,慢车距出发地的距离为60x,
所以此时快、慢两车距各自出发地的路程不可能相等,
当4<x<7时,快车距出发地的距离为:-120x+840,
慢车距出发地的距离为60x,
由-120x+840=60x,
解得x=
.
答:出发
小时,快、慢两车距各自出发地的路程相等.
∵由图可得出两地相距360km,
∴快车速度为:360×2÷6=120(km/h),
慢车速度为:360÷6=60(km/h);
(2)∵快车速度为:120km/h,
∴360÷120=3(h),
∴A点坐标为;(3,360)
∴B点坐标为(4,360),
可得E点坐标为:(6,360),D点坐标为:(7,0),
∴设BD解析式为:y=kx+b,
|
解得:
|
∴BD解析式为:y=-120x+840,
设OE解析式为:y=ax,
∴360=6a,
解得:a=60,
∴OE解析式为:y=60x;
(3)当0<x<3时,
快车距出发地的距离为120x,慢车距出发地的距离为60x,
所以此时快、慢两车距各自出发地的路程不可能相等,
当4<x<7时,快车距出发地的距离为:-120x+840,
慢车距出发地的距离为60x,
由-120x+840=60x,
解得x=
| 14 |
| 3 |
答:出发
| 14 |
| 3 |
点评:此题主要考查了一次函数的应用以及函数交点坐标求法等知识,根据已知图象得出点的坐标是解题关键.

练习册系列答案
相关题目
 已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.
已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.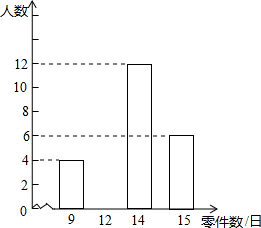 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题: 按图1中所示程序进行计算:
按图1中所示程序进行计算: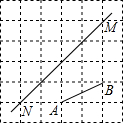 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.