题目内容
 已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.
已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,DF⊥BC于F.求证:AE•BF•AB=CD3.考点:相似三角形的判定与性质
专题:证明题
分析:在直角△ABC、直角△ACD和直角△BCD中应用射影定理,再将线段进行等量代换即可证明.
解答:证明:∵Rt△ABC中,∠ACB=90°,CD⊥AB,∴CD2=AD•BD.∴CD4=AD2•BD2.
又∵Rt△ADC中,DE⊥AC,Rt△BDC中,DF⊥BC,
∴AD2=AE•AC,BD2=BF•BC.
∴CD4=AE•BF•AC•BC.
又∵AC•BC=AB•CD,
∴CD4=AE•BF•AB•CD.
∴AE•BF•AB=CD3.
又∵Rt△ADC中,DE⊥AC,Rt△BDC中,DF⊥BC,
∴AD2=AE•AC,BD2=BF•BC.
∴CD4=AE•BF•AC•BC.
又∵AC•BC=AB•CD,
∴CD4=AE•BF•AB•CD.
∴AE•BF•AB=CD3.
点评:本题考查了相似三角形的性质,正确记忆射影定理的内容是关键.

练习册系列答案
相关题目
下列调查方式,合适的是( )
| A、要了解电视台2014年“春节联欢晚会”栏目的收视率,采用普查方式 |
| B、要了解人们对环境的保护意识,采用抽查方式 |
| C、要保证“神舟十号”载人飞船成功发射,对重要零部件的检查采用抽查方式 |
| D、要了解一批灯泡的使用寿命,采用普查方式 |
如果反比例函数的图象经过点(10,1),那么下列各点中在此反比例函数图象上的点是( )
| A、(-2,5) |
| B、(3,-4) |
| C、(-5,-2) |
| D、(1,-10) |
 如图,是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是100m,则水库大坝的高度h是 ( )
如图,是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是100m,则水库大坝的高度h是 ( )A、50
| ||||
| B、50m | ||||
C、50
| ||||
D、
|
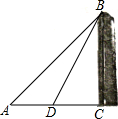 津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(
津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB( 快、慢两车分别从相距360千米的甲乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后安原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)之间的关系如图,请结合图象信息解答下列问题:
快、慢两车分别从相距360千米的甲乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后安原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)之间的关系如图,请结合图象信息解答下列问题: