题目内容
2. 如图,已知直线l1:y=-x+5,直线l2:y=2x+2,两直线交于点A,l1交x轴于C点,l2交y轴于点B,交x轴于点D.
如图,已知直线l1:y=-x+5,直线l2:y=2x+2,两直线交于点A,l1交x轴于C点,l2交y轴于点B,交x轴于点D.(1)求出A、B、C三点的坐标;
(2)求△ABC的面积.
分析 (1)联立两直线解析式求出交点A的坐标,求出l1交x轴于C点,l2交y轴于点B的坐标即可;
(2)三角形ABC面积等于三角形ADC面积减去三角形BCD面积,求出即可.
解答 解:(1)联立得:$\left\{\begin{array}{l}{y=-x+5}\\{y=2x+2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即A(1,4),
对于直线l1:y=-x+5,令y=0,得到x=5,即C(5,0),对于直线l2:y=2x+2,令x=0,得到y=2,即B(0,2);
(2)对于直线l2:y=2x+2,令y=0,得到x=-1,即D(-1,0),
∴CD=5-(-1)=5+1=6,
则S△ABC=S△ADC-S△BDC=$\frac{1}{2}$×6×4-$\frac{1}{2}$×6×2=12-6=6.
点评 此题考查了两条直线相交或平行问题,以及一次函数与坐标轴的交点,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.计算(-9)+6的结果是( )
| A. | 15 | B. | -15 | C. | 3 | D. | -3 |
12.估算$\sqrt{24}$-3的值,在( )
| A. | 在1与2之间 | B. | 在2与3之间 | C. | 在3与4之间 | D. | 在4与5之间 |
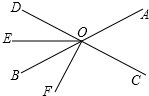 如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.