题目内容
阅读下列材料，并解决后面的问题。
材料：我们知道，n个相同的因数a相乘
可记为an，如23＝8，此时，3叫做以2为底8的对数，记为log28（即log28=3)
一般地，若an=b (a>0且a≠1,b>0)，则n叫做以a为底b的对数，记为logab(即logab=n).如34=81，则4叫做以3为底81的对数，记为log381(即log381=4)
(1)计算以下各对数的值：log24= ，log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式？log24、log216、log264之间又满足怎样的关系式？
(3)根据(2)的结果，我们可以归纳出：logaM+logaN=logaM N (a>0且a≠1,M>0，N>0)，请你根据幂的运算法则：am=an+m以及对数的定义证明该结论。
练习册系列答案
相关题目
9．观察下表：
（1）结合该表格及相关知识，求x，y；
（2）猜想第n行的三个数（用含n的式子表示），并证明它们是一组勾股数．
| 4 | 3 | 5 | 32+42=52 |
| 6 | 8 | 10 | 62+82=102 |
| 8 | 15 | 17 | 82+152=172 |
| 10 | 24 | 26 | 102+242=262 |
| … | … | … | … |
| 60 | x | y | 602+x2=y2 |
| … | … | … | … |
（2）猜想第n行的三个数（用含n的式子表示），并证明它们是一组勾股数．
的值为零，那么x=__________．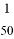
，说明毎买50张奖券中一定有一张中奖
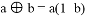，若a、b是方程
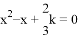(k＜0)的两根，则
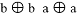的值为______.