题目内容
4. 如图,在△ABC中,点D在BC上,且BD=2CD,AB⊥AD,若tanB=$\frac{4}{3}$,则tan∠CAD=( )
如图,在△ABC中,点D在BC上,且BD=2CD,AB⊥AD,若tanB=$\frac{4}{3}$,则tan∠CAD=( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
分析 作CE⊥AD交AD的延长线于点E,画出相应的图形,然后可以得到各边之间的关系,从而可以表示出tan∠CAD,从而得到tan∠CAD的值.
解答 解:作CE⊥AD交AD的延长线于点E,如下图所示,
∵AB⊥AD,CE⊥AD,
∴∠BAD=∠CED=90°,
∵∠ADB=∠EDC,
∴△BAD∽△CED,
∴∠B=∠DCE,
设AD=4x,AB=3x,
则BD=$\sqrt{A{D}^{2}+A{B}^{2}}=\sqrt{(4x)^{2}+(3x)^{2}}$=5x,
∵BD=2CD,
∴CD=2.5x,
∵tanB=$\frac{4}{3}$,∠B=∠DCE,CD=2.5x,
∴tan∠DCE=$\frac{4}{3}$,sin∠DCE=$\frac{DE}{CD}$=$\frac{4}{5}$,cos$∠DCE=\frac{CE}{CD}$=$\frac{3}{5}$,
∴CE=1.5x,DE=2x,
∴tan∠CAD=$\frac{CE}{AE}=\frac{CE}{AD+AE}=\frac{1.5x}{4x+2x}$=$\frac{1.5x}{6x}=\frac{1}{4}$,
故选B.
点评 本题考查解直角三角形,解题的关键是明确题意,找出各边之间的关系,然后找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列分式中最简分式的是( )
| A. | $\frac{x-y}{{{x^2}-{y^2}}}$ | B. | $\frac{a-2a}{a}$ | C. | $\frac{2a-6b}{2a}$ | D. | $\frac{{{x^2}+{y^2}}}{x+y}$ |
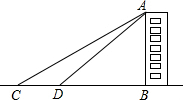 某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进20米到达点D,又测得点A的仰角为45°,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据$\sqrt{2}≈1.414,\sqrt{3}$≈1.732)
某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进20米到达点D,又测得点A的仰角为45°,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据$\sqrt{2}≈1.414,\sqrt{3}$≈1.732) 如图,已知由x轴、一次函数y=kx+4(k<0)的图象及分别过点C(1,0)、D(4,0)两点作平行于y轴的两条直线所围成的图形ABDC的面积为7,试求这个一次函数的解析式.
如图,已知由x轴、一次函数y=kx+4(k<0)的图象及分别过点C(1,0)、D(4,0)两点作平行于y轴的两条直线所围成的图形ABDC的面积为7,试求这个一次函数的解析式. 如图,点C是线段AB上一点,AC<AB,M,N分别是AB和CB的中点,AC=8,NB=5,求线段MN的长.
如图,点C是线段AB上一点,AC<AB,M,N分别是AB和CB的中点,AC=8,NB=5,求线段MN的长.
