题目内容
7. 已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.
已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.
分析 由相似三角形的性质易证∠1=∠2,再由三角形内角和定理易证∠2=∠3,进而可证明∠1=∠2=∠3.
解答 证明:∵△ABC∽△ADE,
∴∠C=∠E,∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠1=∠2,
在△AOE和△DOC中,
∠E=∠C,∠AOE=∠DOC(对顶角相等),
∴∠2=∠3,
∴∠1=∠2=∠3.
点评 本题考查了相似三角形的性质,熟记相似三角形的各种性质是解题关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.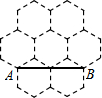 如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的各顶点称为格点,直角△ABC的顶点均在格点上,则满足条件的点C有( )
如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的各顶点称为格点,直角△ABC的顶点均在格点上,则满足条件的点C有( )
 如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的各顶点称为格点,直角△ABC的顶点均在格点上,则满足条件的点C有( )
如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的各顶点称为格点,直角△ABC的顶点均在格点上,则满足条件的点C有( )| A. | 6个 | B. | 8个 | C. | 10个 | D. | 12个 |
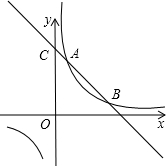 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求:
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A(1,4)和点B,与y轴交于点C(0,5).求: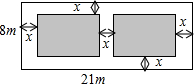 某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?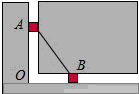 图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.
图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.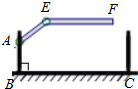 某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )
某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:$\sqrt{2}$≈1.4)( )


