题目内容
19.(1)x2-2x=4(配方法)(2)5x2+2x-1=0 (公式法)
(3)2(x-3)2=x2-9(因式分解法)
(4)(x-$\sqrt{2}$)2+4$\sqrt{2}$x=0.
分析 (1)配方法求解可得;
(2)公式法求解可得;
(3)因式分解法求解可得;
(4)因式分解法求解可得.
解答 解:(1)∵x2-2x+1=4+1,即(x-1)2=5,
∴x-1=±$\sqrt{5}$,
则x=1$±\sqrt{5}$;
(2)∵a=5,b=2,c=-1,
∴△=4-4×5×(-1)=24>0,
则x=$\frac{-2±2\sqrt{6}}{10}$=$\frac{-1±\sqrt{6}}{5}$;
(3)∵2(x-3)2-(x+3)(x-3)=0,
∴(x-3)(x-9)=0,
则x-3=0或x-9=0,
解得:x=3或x=9;
(4)∵x2-2$\sqrt{2}$x+2+4$\sqrt{2}$x=0,即x2+2$\sqrt{2}$+2=0,
∴(x+$\sqrt{2}$)2=0,
则x+$\sqrt{2}$=0,
解得:x=-$\sqrt{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7.我国西部地区面积为640万平方千米,用科学记数法表示为( )
| A. | 640×104 | B. | 64×106 | C. | 6.4×106 | D. | 6.4×107 |
4.一元二次方程x2+2x+1=0的根的情况( )
| A. | 无法判断 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
9.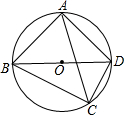 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )| A. | AC=BC+CD | B. | $\sqrt{2}$AC=BC+CD | C. | $\sqrt{3}$AC=BC+CD | D. | 2AC=BC+CD |
 △ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上,作出△ABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标.
△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上,作出△ABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标.