题目内容
11.解方程:$\sqrt{{x}^{2}+7}$-$\sqrt{2}$x=1.分析 先变形为$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,两边平方得到x2+7=2x2+2$\sqrt{2x}$+1,再变形,利用配方法即可解答此无理方程.
解答 解:∵$\sqrt{{x}^{2}+7}$-$\sqrt{2}x$=1,
∴$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,
∴x2+7=2x2+2$\sqrt{2}$x+1
∴x2+2$\sqrt{2}$x-6=0
∴$(x+\sqrt{2})^{2}$=8,
∴$x+\sqrt{2}=±2\sqrt{2}$,
∴x=$-\sqrt{2}±2\sqrt{2}$,
∴${x}_{1}=-3\sqrt{2}$,${x}_{2}=\sqrt{2}$
点评 此题考查了解无理方程,解无理方程关键是要去掉根号,将其转化为整式方程.解无理方程的基本思想是把无理方程转化为有理方程来解,在变形时要注意根据方程的结构特征选择解题方法.

练习册系列答案
相关题目
2.下列各组中的两项是同类项的是( )
| A. | 5zy2和-4y2z | B. | -3m2n和mn2 | C. | -x2和3x | D. | 0.5a和0.5b |
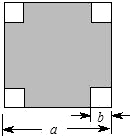 如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.
如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.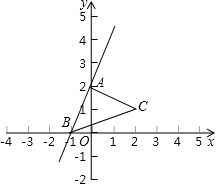 在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).
在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).