题目内容
9.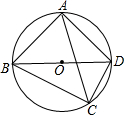 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )| A. | AC=BC+CD | B. | $\sqrt{2}$AC=BC+CD | C. | $\sqrt{3}$AC=BC+CD | D. | 2AC=BC+CD |
分析 在CD延长线上截取DE=BC,连接EA,证明△ABC≌△ADE,得到△EAF是等腰直角三角形即可得出结论.
解答 解:在CD的延长线上截取DE=BC,连接EA,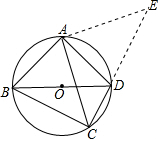
∵∠ABD=∠ACB=∠ABD=45°,
∴AB=AD,
∵∠ADE+∠ADC=180°,
∠ABC+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC与△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABC=∠ADE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE=90°,
∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,
∴$\sqrt{2}$AC=CE,
∴$\sqrt{2}$AC=CD+DE=CD+BC,
故选:B.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、全等三角形的判定定理和性质定理、等腰直角三角形的性质是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
4.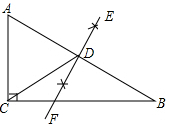 如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
 如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )| A. | 13 | B. | 17 | C. | 18 | D. | 25 |
18.高速路上因赶时间超速而频频发生交通事故,这样给自己和他人的生命安全带来直接影响,为了解车速情况,一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下:
则这6辆车车速的众数和中位数(单位:千米/时)分别是( )
| 车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 车速(千米/时) | 100 | 95 | 106 | 100 | 120 | 100 |
| A. | 100,95 | B. | 100,100 | C. | 102,100 | D. | 100,103 |
19.已知248-1可以被在60~70之间的两个整数整除,则这两个数是( )
| A. | 64,63 | B. | 61,65 | C. | 61,67 | D. | 63,65 |
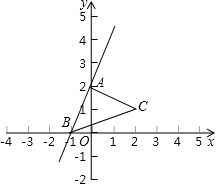 在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).
在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).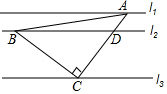 已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,
已知直线l1∥l2∥l3,等腰直角△ABC的三个顶点A,B,C分别在l1,l2,l3上,若∠ACB=90°,l1,l2的距离为1,l2,l3的距离为3,