题目内容
 如图,点A,B,C,D都在⊙O上,
如图,点A,B,C,D都在⊙O上, |
| CD |
考点:圆周角定理
专题:
分析:在等腰△OAC和△OCD中,根据等腰三角形的两个底角相等的性质求得∠OCD=∠ODC、∠CAO=∠OCA,所以由三角形的内角和求得∠OCD=53°;然后根据角平分线的性质求得∠OCA=∠ACD=24°;最后由圆周角定理知:∠ABD=
∠AOD,∠OCA=
∠AOD.所以∠ABD=∠CAO,进而求得∠ABD+∠CAO=53°.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵圆心角的度数和它们对的弧的度数相等,
∴
的度数等于74°,即∠COD=74°;
在△COD中,OC=OD(⊙O的半径),
∴∠OCD=∠ODC(等边对等角);
又∵∠COD+∠OCD+∠ODC=180°,
∴∠OCD=53°;
而CA是∠OCD的平分线,
∴∠OCA=∠ACD,
∴∠OCA=∠ACD=26.5°;
在△AOC中,OA=OC(⊙O的半径),
∴∠CAO=∠OCA(等边对等角);
∵∠ABD=
∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∠DCA=
∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∴∠ABD=∠DCA,
∴∠ABD+∠CAO=53°;
故答案为:53.
∴
 |
| CD |
在△COD中,OC=OD(⊙O的半径),
∴∠OCD=∠ODC(等边对等角);
又∵∠COD+∠OCD+∠ODC=180°,
∴∠OCD=53°;
而CA是∠OCD的平分线,
∴∠OCA=∠ACD,
∴∠OCA=∠ACD=26.5°;
在△AOC中,OA=OC(⊙O的半径),
∴∠CAO=∠OCA(等边对等角);
∵∠ABD=
| 1 |
| 2 |
∠DCA=
| 1 |
| 2 |
∴∠ABD=∠DCA,
∴∠ABD+∠CAO=53°;
故答案为:53.
点评:本题综合考查了圆周角定理和圆心角、弧、弦的关系.解答此题的关键点是利用“圆心角的度数和它所对的弧的度数相等”求得∠COD=74°.

练习册系列答案
相关题目
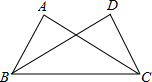 如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )
如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )| A、SAS | B、ASA |
| C、AAS | D、HL |
在平面直角坐标系中,点P(-2,-6)向左平移2单位,再向上平移3个单位后的点的坐标是( )
| A、(0,-3) |
| B、(-4,-3) |
| C、(0,-9) |
| D、(-4,-9) |
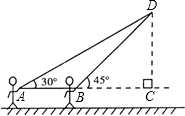 放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)
放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)