题目内容
4. 如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
分析 作EM⊥CD,垂足为点M设DE=x,由折叠的性质得出∠DEF=∠BEF,BE=DE=x,得出AE=8-x,再由矩形的性质得出∠DEF=∠DFE,证出DE=DF,在Rt△ADE中,由勾股定理得出方程,解方程求出DE,得出AE、MF,由勾股定理求出EF即可.
解答 解:作EM⊥CD,垂足为点M,如图所示: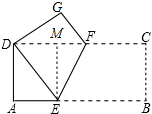
设DE=x,
由折叠的性质得:∠DEF=∠BEF,BE=DE=x,
∴AE=8-x,
∵四边形ABCD是矩形,
∴∠A=90°,AB∥CD,
∴∠DFE=∠BEF,
∴∠DEF=∠DFE,
∴DE=DF,
在Rt△ADE中,由勾股定理得:(8-x)2+62=x2,
解得:x=$\frac{25}{4}$,
∴AE=DM=8-$\frac{25}{4}$=$\frac{7}{4}$,
又∵DF=DE=$\frac{25}{4}$,
∴MF=DF-DM=$\frac{25}{4}$-$\frac{7}{4}$=$\frac{9}{2}$,
又∵ME=AD=6,
∴EF=$\sqrt{M{E}^{2}+M{F}^{2}}$=$\sqrt{{6}^{2}+(\frac{9}{2})^{2}}$=$\frac{15}{2}$.
点评 此题主要考查了翻折变换的性质矩形的性质、勾股定理、等腰三角形的判定;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程求出BE是解决问题的关键.

练习册系列答案
相关题目
 的运算结果应在哪两个连续自然数之间( )
的运算结果应在哪两个连续自然数之间( ) 如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°. 如图,图形B是由图形A旋转得到的,则旋转中心的坐标为(0,1)
如图,图形B是由图形A旋转得到的,则旋转中心的坐标为(0,1)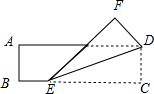 将一张长方形纸片ABCD按如图所示折叠,使顶点C落在点F处,已知AB=2,∠DEF=30°,则折痕DE的长度为( )
将一张长方形纸片ABCD按如图所示折叠,使顶点C落在点F处,已知AB=2,∠DEF=30°,则折痕DE的长度为( )