题目内容
15.已知实数m、n满足m2=2-2m,n2=2-2n,则$\frac{m}{n}$+$\frac{n}{m}$=-4或2.分析 分两种情况:①当m=n时,②由m≠n时,得到m,n是方程x2+2x-2=0的两个不等的根,根据根与系数的关系进行求解.
解答 解:①当m=n时,$\frac{m}{n}$+$\frac{n}{m}$=2;
②当m≠n时,则m,n是方程x2+2x-2=0的两个不相等的根,∴m+n=-2,mn=-2,
∴$\frac{m}{n}$+$\frac{n}{m}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{4+4}{-2}$=-4,
∴$\frac{m}{n}$+$\frac{n}{m}$=-4或2,
故答案为:-4或2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
5.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{3{x}^{2}+y=1}\\{10x-8y=-9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=2}\\{\frac{1}{x}-3y=-\frac{7}{4}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=1}\\{2x-y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{xy=4}\\{x+2y=6}\end{array}\right.$ |
3.已知(x-2y-1)2+|2x+y-7|=0,则3x-y=( )
| A. | 3 | B. | 1 | C. | 8 | D. | -6 |
 如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°.
如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度. ×3
×3 =6
=6 B.
B.  +
+ =
=
 -2
-2 =3
=3 D.
D.  ÷
÷ =
=
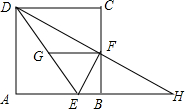 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论: 如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.
如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.