题目内容
9.($\frac{{x}^{2}-2x+4}{x-1}$+2-x)÷$\frac{{x}^{2}+4x+4}{1-x}$=-$\frac{1}{x+2}$.分析 先计算括号内分式的加法,再将除法转化为乘法,最后计算乘法即可.
解答 解:原式=[$\frac{{x}^{2}-2x+4}{x-1}$+$\frac{(x-1)(2-x)}{x-1}$]•$\frac{1-x}{(x+2)^{2}}$
=[$\frac{{x}^{2}-2x+4}{x-1}$+$\frac{-{x}^{2}+3x-2}{x-1}$]•$\frac{1-x}{(x+2)^{2}}$
=$\frac{x+2}{x-1}$•$\frac{1-x}{(x+2)^{2}}$
=-$\frac{1}{x+2}$.
故答案为:-$\frac{1}{x+2}$.
点评 本题主要考查分式的混合运算,熟练掌握分式的混合运算顺序和运算法则是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
13.无理数-$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | -$\frac{1}{\sqrt{2}}$ |
16.若$\sqrt{1-2x}$有意义,则x的取值范围( )
| A. | x>2 | B. | x≤$\frac{1}{2}$ | C. | x≠$\frac{1}{2}$ | D. | x≤2 |
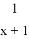 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )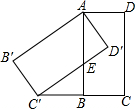 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E. 如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.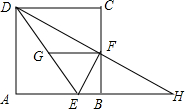 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论: 已知:线段a,h.
已知:线段a,h.