题目内容
12.化简:($\frac{b}{a+b}$+$\frac{b}{a-b}$)÷$\frac{a}{a^2-b^2}$.分析 首先把除法转化为乘法,然后利用分配律计算,再通分相加即可求解.
解答 解:原式=($\frac{b}{a+b}$+$\frac{b}{a-b}$)•$\frac{(a+b)(a-b)}{a}$
=$\frac{b}{a+b}$•$\frac{(a+b)(a-b)}{a}$+$\frac{b}{a-b}$•$\frac{(a+b)(a-b)}{a}$
=$\frac{b(a-b)}{a}$+$\frac{b(a+b)}{a}$
=$\frac{ab-{b}^{2}+ab+{b}^{2}}{a}$
=2b.
点评 本题考查了分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
5.已知x2-2x-2015=0,那么代数式2x2-4x-2016的值为( )
| A. | 2011 | B. | 2013 | C. | 2014 | D. | 2015 |
19.估计二次根式$\sqrt{3}$在整数( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
 ,求证:BC=DE.
,求证:BC=DE.
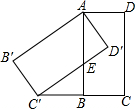 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E. 如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°.
如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.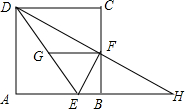 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论: