题目内容
16.设m2+1=3m,n2+1=3n,且m≠n,则代数式$\frac{1}{{m}^{2}}$+$\frac{1}{{n}^{2}}$的值是( )| A. | 5 | B. | 9 | C. | 7 | D. | 11 |
分析 根据条件得到m、n是方程x2-3x+1=0的两个根,由此可以根据根与系数关系解决问题.
解答 解:∵m2+1=3m,n2+1=3n,且m≠n,
∴m、n是方程x2-3x+1=0的两个根,
∴m+n=3,mn=1,
∴$\frac{1}{{m}^{2}}$+$\frac{1}{{n}^{2}}$=$\frac{(m+n)^{2}-2mn}{(mn)^{2}}$=$\frac{9-2}{1}$=7.
故选C.
点评 本题考查根与系数关系、整体代入的思想,解题的关键是学会转化的思想,把问题转化为一元二次方程解决,学会利用公式恒等变形,属于中考常考题型.

练习册系列答案
相关题目
5.已知x2-2x-2015=0,那么代数式2x2-4x-2016的值为( )
| A. | 2011 | B. | 2013 | C. | 2014 | D. | 2015 |
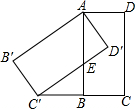 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
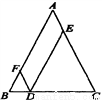
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E. 如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°.
如图,△ABC和△ADC分别在AC的两侧,∠BAC:∠B:∠ACB=4:3:2,且∠DAC=40°. 如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度. 如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.
如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.