题目内容
8.正六边形的外接圆半径为1,则它的内切圆半径为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
解答 解:如图,连接OA、OB,OG;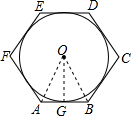
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴∠OAB=60°,
∴OG=OA•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴半径为2的正六边形的内切圆的半径为$\frac{\sqrt{3}}{2}$.
故选B.
点评 本题考查了正多边形和圆、等边三角形的判定与性质;熟练掌握正多边形的性质,证明△OAB是等边三角形是解决问题的关键.

练习册系列答案
相关题目
18.下列图形中主视图,左视图不相同的是( )
| A. |  | B. |  | C. |  | D. |  |
19.合作交流是学习数学的重要方式之一,某校九年级每班的合作学习小组的个数分别是:8,7,7,8,9,7,则由这组数据得到的结论中错误的是( )
| A. | 平均数是7 | B. | 中位数是7.5 | C. | 众数是7 | D. | 极差是2 |
16. 长方体的主视图、俯视图如图所示,则长方体的表面积为( )
长方体的主视图、俯视图如图所示,则长方体的表面积为( )
 长方体的主视图、俯视图如图所示,则长方体的表面积为( )
长方体的主视图、俯视图如图所示,则长方体的表面积为( )| A. | 12 | B. | 19 | C. | 24 | D. | 38 |
3.一个几何体的三视图如图所示,该几何体的侧面积为( )
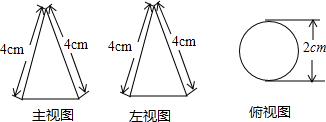

| A. | 2πcm2 | B. | 4πcm2 | C. | 8πcm2 | D. | 16πcm2 |
13.一个等腰三角形的两条边长分别是方程x2-3x+2=0的两根,则该等腰三角形的周长是( )
| A. | 5或4 | B. | 4 | C. | 5 | D. | 3 |
18.根据PM2.5空气质量标准:24小时PM2.5均值在0∽35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,这组PM2.5数据的中位数是( )
| 天数 | 3 | 1 | 1 | 1 | 1 |
| PM2.5 | 18 | 20 | 21 | 29 | 30 |
| A. | 21微克/立方米 | B. | 20微克/立方米 | C. | 19微克/立方米 | D. | 18微克/立方米 |