题目内容
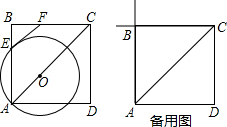 如图,点O在边长为6
如图,点O在边长为6| 2 |
(1)⊙O过点E的○切线与BC交于点F,当0<OA<6时,求∠BFE的度数;
(2)设⊙O与AB的延长线交于点M,⊙O过点M的切线交BC的延长线于点N,当6<OA<12时,利用备用图作出图形,求∠BNM的度数;
(3)在(2)条件下,求出当点O与C点重合时DM的长.
考点:切线的性质,勾股定理,正方形的性质
专题:
分析:(1)连结OE,根据正方形的性质得∠2=45°,再由OE=OA得到∠1=∠2=45°,然后根据切线的性质得∠OEF=90°,则∠BEF=45°,易得∠BFE=45°;
(2)连结OM,由OM=OA得到∠OMA=∠OAM=45°,再根据切线的性质得∠OMN=90°,则∠BMN=45°,易得∠BNM=45°;
(3)连结CM、DM,由于∠CMA=∠CAM=45°,则△CMA为等腰直角三角形,所以AM=
AC,根据正方形的性质由正方形ABCD的边长为6
得到AC=
×6
=12,所以AM=12
,然后在Rt△ADM中根据勾股定理计算DM.
(2)连结OM,由OM=OA得到∠OMA=∠OAM=45°,再根据切线的性质得∠OMN=90°,则∠BMN=45°,易得∠BNM=45°;
(3)连结CM、DM,由于∠CMA=∠CAM=45°,则△CMA为等腰直角三角形,所以AM=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答: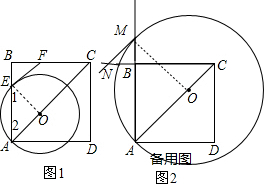 解:(1)连结OE,如图1,
解:(1)连结OE,如图1,
∵四边形ABCD为正方形,
∴∠2=45°,
∵OE=OA,
∴∠1=∠2=45°,
∵EF为⊙O的切线,
∴OE⊥EF,
∴∠OEF=90°,
∴∠BEF=45°,
而∠B=90°,
∴∠BFE=45°;
(2)连结OM,如图2,
∵OM=OA,
∴∠OMA=∠OAM=45°,
∵MN为⊙O的切线,
∴OM⊥MN,
∴∠OMN=90°,
∴∠BMN=45°,
而∠MBN=90°,
∴∠BNM=45°;
(3)连结CM、DM,如图3,
∵∠CMA=∠CAM=45°,
∴△CMA为等腰直角三角形,
∴AM=
AC,
∵正方形ABCD的边长为6
,
∴AC=
×6
=12,
∴AM=12
,
在Rt△ADM中,DM=
=
=6
.
 解:(1)连结OE,如图1,
解:(1)连结OE,如图1,∵四边形ABCD为正方形,
∴∠2=45°,
∵OE=OA,
∴∠1=∠2=45°,
∵EF为⊙O的切线,
∴OE⊥EF,
∴∠OEF=90°,
∴∠BEF=45°,
而∠B=90°,
∴∠BFE=45°;
(2)连结OM,如图2,
∵OM=OA,
∴∠OMA=∠OAM=45°,
∵MN为⊙O的切线,
∴OM⊥MN,

∴∠OMN=90°,
∴∠BMN=45°,
而∠MBN=90°,
∴∠BNM=45°;
(3)连结CM、DM,如图3,
∵∠CMA=∠CAM=45°,
∴△CMA为等腰直角三角形,
∴AM=
| 2 |
∵正方形ABCD的边长为6
| 2 |
∴AC=
| 2 |
| 2 |
∴AM=12
| 2 |
在Rt△ADM中,DM=
| AM2+AD2 |
(12
|
| 10 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理和正方形的性质.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

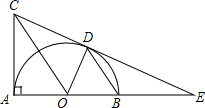 如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E.
如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E. 已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC.
已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC.