题目内容
6.已知抛物线y=x2-x-1与x轴的一个交点的横坐标为m,则代数式m2-m+2016的值为2017.分析 把点(m,0)代入抛物线的解析式得到m2-m=1,整体代入即可解决问题.
解答 解:∵抛物线y=x2-x-1与x轴的一个交点为(m,0),
∴m2-m-1=0,
∴m2-m=1,
∴m2-m+2016=1-2013=-2017,
故答案为2017.
点评 本题考查抛物线与x轴的交点,待定系数法等知识,解题的关键是学会利用整体代入法解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.将一个正方体的表面沿某些棱剪开,展成一个平面图形,至少要剪开( )条棱.
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
1. 如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )
如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )
 如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )
如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 10$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
16.若$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$,则$\frac{2{a}^{2}-3bc+{c}^{2}}{{a}^{2}-2ab-{c}^{2}}$的值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
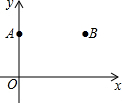 如图,已知点A(0,4)、点B(6,4),点C在x轴上,若△ABC是等腰三角形,则点C的横坐标为$6-2\sqrt{5}$或$6+2\sqrt{5}$或3或$-2\sqrt{5}$或$2\sqrt{5}$.
如图,已知点A(0,4)、点B(6,4),点C在x轴上,若△ABC是等腰三角形,则点C的横坐标为$6-2\sqrt{5}$或$6+2\sqrt{5}$或3或$-2\sqrt{5}$或$2\sqrt{5}$.