题目内容
13.已知m+n+p=0,且m>n>p,则$\frac{p}{m}$的取值范围是-2<$\frac{p}{m}$<-1或$\frac{p}{m}$>-1.分析 首先由m+n+p=0,得出p=-m-n,进一步推出$\frac{p}{m}$=-1-$\frac{n}{m}$,分n>0和n<0两种请情况探讨得出答案即可.
解答 解:∵m+n+p=0,
∴p=-m-n,
∴$\frac{p}{m}$=$\frac{-m-n}{m}$=-1-$\frac{n}{m}$,
∵m+n+p=0,且m>n>p,
∴m>0,p<0,
当n>0时,
∵m>n,
∴0<$\frac{n}{m}$<1,
∴-1<-$\frac{n}{m}$<0,
∴-2<-1-$\frac{n}{m}$<-1,
∴-2<$\frac{p}{m}$<-1;
当n<0时,$\frac{n}{m}$<0,
∵-$\frac{n}{m}$>0,
∴-1-$\frac{n}{m}$>-1
∴$\frac{p}{m}$>-1.
故答案为:-2<$\frac{p}{m}$<-1或$\frac{p}{m}$>-1.
点评 此题考查不等式的性质,利用代换的方法得出m、n的关系,进一步分类探讨得出答案即可.

练习册系列答案
相关题目
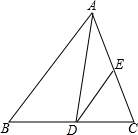 如图,∠B=∠CAD,CD2=CE•AC,AE=4,AD=9,BD=5,求AB的长.
如图,∠B=∠CAD,CD2=CE•AC,AE=4,AD=9,BD=5,求AB的长.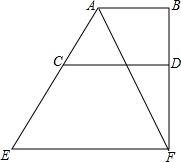 如图,AB⊥BF,CD⊥BF.∠BAF=∠AFE,求证:∠DCE+∠E=180°.
如图,AB⊥BF,CD⊥BF.∠BAF=∠AFE,求证:∠DCE+∠E=180°.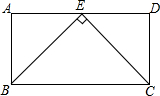 如图,在矩形ABCD中,E是AD的中点,连接BE,CE,且BE⊥CE.若矩形的周长为18cm,求矩形各边的长.
如图,在矩形ABCD中,E是AD的中点,连接BE,CE,且BE⊥CE.若矩形的周长为18cm,求矩形各边的长.