题目内容
9．
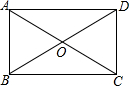如图，在矩形ABCD中，已知AB=4，OA=3，则BC的长度为（ ）| A． | 5 | B． | $2\sqrt{5}$ | C． | $2\sqrt{13}$ | D． | $\sqrt{13}$ |
分析 直接利用矩形的性质得出AC的长，再利用勾股定理得出BC的长．
解答 解：∵在矩形ABCD中，AB=4，OA=3，
∴AC=6，∠ABC=90°
则BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$．
故选：B．
点评 此题主要考查了矩形的性质以及勾股定理，正确得出AC的长是解题关键．
练习册系列答案
相关题目
8．某人沿倾斜角为30°的斜坡前进6米，则他上升的最大高度为（ ）
| A． | 3米 | B． | 3$\sqrt{3}$米 | C． | $\sqrt{3}$米 | D． | 2$\sqrt{3}$米 |
14．（-0.25）2014×42013等于（ ）
| A． | -4 | B． | 4 | C． | 0.25 | D． | -0.25 |
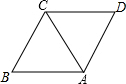如图，在菱形ABCD中，对角线AC=4，∠B=60°，则菱形ABCD面积为8$\sqrt{3}$．
18．
如图所示，P是反比例函数y=的图象上一点，过点P分别向x轴和y轴引垂线，若S阴影=3，则k的值是（ ）
如图所示，P是反比例函数y=的图象上一点，过点P分别向x轴和y轴引垂线，若S阴影=3，则k的值是（ ）| A． | 3 | B． | -3 | C． | ±3 | D． | -9 |