题目内容
19．用反证法证明“四边形的四个内角不能都是锐角”时，应首先假设四边形的四个内角都是锐角，再证明与“四边形的四个内角和等于360度”相矛盾．分析 直接利用反证法的第一步，从结论的反面出发进行假设得出答案．
解答 解：用反证法证明“四边形的四个内角不能都是锐角”时，应首先假设四边形的四个内角都是锐角．
故答案为：四边形的四个内角都是锐角．
点评 此题主要考查了反证法，正确把握反证法的一般步骤是解题关键．
练习册系列答案
相关题目
9．
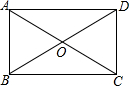如图，在矩形ABCD中，已知AB=4，OA=3，则BC的长度为（ ）
如图，在矩形ABCD中，已知AB=4，OA=3，则BC的长度为（ ）| A． | 5 | B． | $2\sqrt{5}$ | C． | $2\sqrt{13}$ | D． | $\sqrt{13}$ |
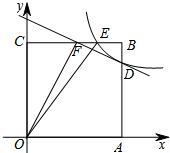如图，正方形OABC的边长为4，反比例函数y=$\frac{k}{x}$（k＞0）的图象与线段AB交于点D，与线段BC交于点E，点E的坐标为（3，4）．
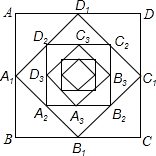连结正方形四边中点所构成的正方形，我们称其原正方形的中点正方形，如图，已知正方形ABCD的中点正方形是A1B1C1D1，再作正方形A1B1C1D1的中点正方形A2B2C2D2，…这样不断地作下去，第n次所做的中点正方形 AnBnCnDn，若正方形ABCD的边长为1，则第10次所作的中点正方形边长为$\frac{1}{32}$，若设中点正方形 AnBnCnDn的面积为Sn，则S1+S2+S3+…+S10=$\frac{1023}{1024}$．
11．若一个正数的平方根是2a-1和-a+2，则这个正数是（ ）
| A． | 1 | B． | 3 | C． | 4 | D． | 9 |
如图，在正方形ABCD中，点E、F分别在BC、CD上，且BE=DF，若∠EAF=30°，则sin∠EDF=$\frac{（\sqrt{3}-1）\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$．
9．
如图，在?ABCD中，BE平分∠ABC，BC=6，DE=2，则?ABCD的周长等于（ ）
如图，在?ABCD中，BE平分∠ABC，BC=6，DE=2，则?ABCD的周长等于（ ）| A． | 20 | B． | 18 | C． | 16 | D． | 14 |