题目内容
14.若一个多边形的内角和是其外角和的4倍,则此多边形的对角线共有( )| A. | 35条 | B. | 40条 | C. | 10条 | D. | 50条 |
分析 任何多边形的外角和是360度,内角和是外角和的4倍,则内角和是4×360度.n边形的内角和是(n-2)•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数,即可得到结论.
解答 解:设边数为n,则
(n-2)•180°=4×360°,
解得:n=10.
则多边形的边数是10,
故多边形的对角线共有$\frac{10×(10-3)}{2}$=35条.
故选A.
点评 本题考查了多边形的内角和公式与外角和定理,多边形的外角和与边数无关,任何多边形的外角和都是360°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列命题正确的是( )
| A. | 同位角相等 | B. | 如果x2=y2,那么x=y | ||
| C. | 如果a=0,那么ab=0 | D. | 相等的角是对顶角 |
19.下列各点中,在第四象限的点是( )
| A. | (1,3) | B. | (1,-3) | C. | (-1,-3) | D. | (-1,3) |
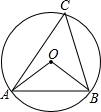 如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.
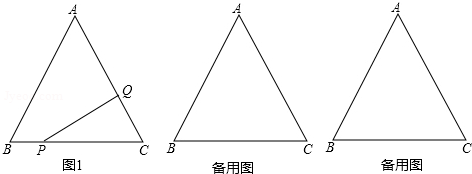
如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度. 若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )
若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )



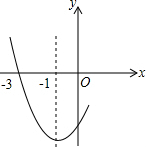 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )