题目内容
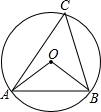
13．
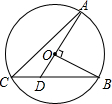如图，OA，OB是⊙O的半径，且OA⊥OB，AO的延长线与弦BC交于点D，连结AC．若∠B=25°，则∠A的度数是（ ）| A． | 65° | B． | 45° | C． | 25° | D． | 20° |
分析 由OA⊥OB，利用圆周角定理，可求得∠C的度数，由三角形外角的性质，可求得∠ADB的度数，继而求得∠A的度数．
解答 解：∵OA⊥OB，
∴∠AOB=90°，
∴∠C=$\frac{1}{2}$∠AOB=45°，∠ADB=∠AOB-∠B=90°-25°=65°，
∴∠A=∠ADB-∠C=20°．
故选D．
点评 此题考查了圆周角定理以及三角形外角的性质．注意在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
3．
如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=50°，则∠P=（ ）
如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=50°，则∠P=（ ）| A． | 100° | B． | 80° | C． | 60° | D． | 50° |
8．
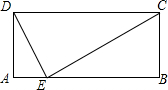矩形ABCD中，AD=5，DC=12，在AB上找一点E，使点E与点C、点D的连线将此矩形分成三个相似三角形．这样的点存在吗？（ ）
矩形ABCD中，AD=5，DC=12，在AB上找一点E，使点E与点C、点D的连线将此矩形分成三个相似三角形．这样的点存在吗？（ ）| A． | 有一个点 | B． | 有两个点 | C． | 不存在 | D． | 无法确定 |
18．
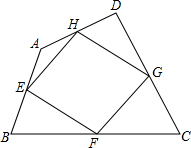如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．若四边形ABCD的面积记为S1，中点四边形EFGH的面积记为S2，则S1与S2的数量关系是（ ）
如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．若四边形ABCD的面积记为S1，中点四边形EFGH的面积记为S2，则S1与S2的数量关系是（ ）| A． | S1=3S2 | B． | 2S1=3S2 | C． | S1=2S2 | D． | 3S1=4S2 |
如图，锐角△ABC的顶点A，B，C都在⊙O上，∠OAB=25°，则∠C的度数为65度．
若正比例函数y=kx的图象如图所示，则一次函数y=x+k的图象大致是（ ）
