题目内容
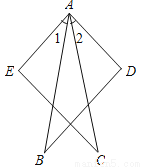
如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
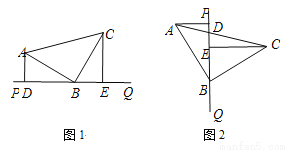
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD,DE,CE有怎样的等量关系?说明理由.
(1)△ADB≌△BEC,(2)CE+AD=DE,(3)CE-AD=DE, 【解析】试题分析:(1)求出∠ADB=∠ABC=∠BEC=90°,求出∠DAB=∠CBE,根据AAS推出△ADB≌△BEC即可; (2)根据全等得出AD=BE,CE=DB,即可求出答案; (3)证明过程和(1)(2)类似. 试题解析:(1)△ADB≌△BEC, 理由是:∵AD⊥PQ,CE⊥PQ...
练习册系列答案
相关题目
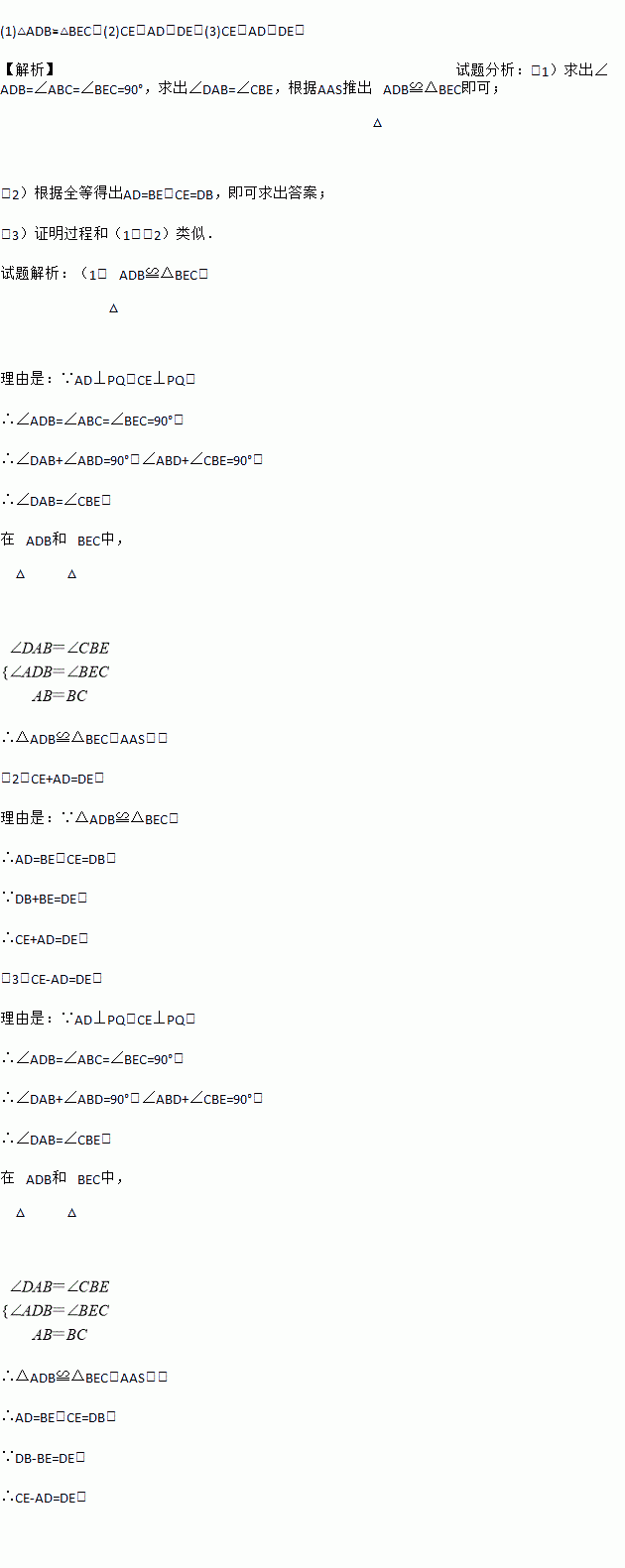

 ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )
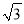 B. 3+
B. 3+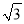 C. 4+
C. 4+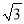 D. 5+
D. 5+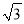
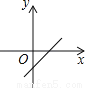 B.
B. 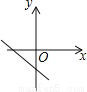 C.
C. 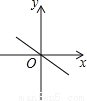 D.
D. 
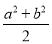 -ab=___________________________.
-ab=___________________________.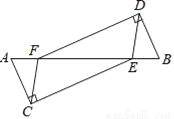
 圆柱 B.
圆柱 B.  球 C.
球 C.  圆锥 D.
圆锥 D.  长方体
长方体