题目内容
16．
如图，在?ABCD中，AC、BD相交于O，F在BC延长线上，交CD于E，如果OE=EF，则BF：CF等于（ ）| A． | 3：1 | B． | 2：1 | C． | 5：2 | D． | 3：2 |
分析 过O作OH∥CD，交BC于点H，利用平行线的性质，可知H为BC的中点，C为HF的中点，可求得BF=3CF，可求得答案．
解答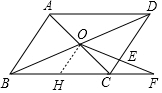 
解：
如图，过O作OH∥CD，交BC于点H，
∵四边形ABCD为平行四边形，
∴O为BD中点，
∴H为BC中点，
∵OE=EF，
∴E为OF的中点，
∴C为HF的中点，
∴BH=HC=CF，
∴BF=3CF，
∴BF：CF=3：1，
故选A．
点评 本题主要考查平行线分线段成比例的性质，由平行四边形的性质结合平行线分线段成比例的性质，求得H、C是BF的三等分点是解题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
6．某商店在出售某种商品时，以m元的价格出售，亏本20%，则在这次买卖中该商店的亏损情况是（ ）
| A． | 亏20%m元 | B． | 亏80%m元 | C． | 亏25%m元 | D． | 亏20%元 |
7．
如图，BE、CF分别是△ABC的高，M为BC的中点，若EF=10，BC=14，则△EFM的周长是（ ）
如图，BE、CF分别是△ABC的高，M为BC的中点，若EF=10，BC=14，则△EFM的周长是（ ）| A． | 17 | B． | 19 | C． | 24 | D． | 34 |
11．
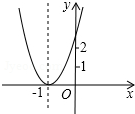已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（-1，0），下列结论：①abc＜0；②4ac-b2=0；③a＞2；④4a-2b+c＞0．其中正确的个数是（ ）
已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（-1，0），下列结论：①abc＜0；②4ac-b2=0；③a＞2；④4a-2b+c＞0．其中正确的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
如图，点P为∠AOB内一点，分别作出点P关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N．若∠AOB=30°，则∠P1OP2=60°．
8．下列各式：$\frac{1}{a}$，$\frac{a+b}{7a}$，x2+$\frac{1}{2}$y2，$\frac{1}{2}$，$\frac{1}{x+1}$，$\frac{x+2}{8π}$，$\frac{{{a^2}-1}}{a+1}$中，分式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
5．
如图，在菱形ABCD中，∠BCD=80°，BC的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠ADF等于（ ）
如图，在菱形ABCD中，∠BCD=80°，BC的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠ADF等于（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
如图，在矩形ABCD中，AB=4，BC=8，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）