题目内容
11.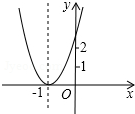 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②4ac-b2=0;③a>2;④4a-2b+c>0.其中正确的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②4ac-b2=0;③a>2;④4a-2b+c>0.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据二次函数的图象以及顶点坐标,分别找出a、b、c之间的关系,对照4条结论判断其正确与否,由此即可得出结论.
解答 解:①∵抛物线开口朝上,
∴a>0.
∵抛物线的对称轴为x=-$\frac{b}{2a}$=-1,
∴b=2a>0.
当x=0时,y=c+2>2,
∴c>0.
∴abc>0,①错误;
②∵抛物线与x轴只有一个交点,
∴b2-4a(c+2)=b2-4ac-8a=0,
∴b2-4ac=8a>0,②错误;
③∵抛物线的顶点为(-1,0),
∴抛物线解析式为y=a(x+1)2=ax2+2ax+a=ax2+bx+c+2,
∴a=c+2>2,③正确;
④∵b=2a,c>0,
∴4a-2b+c=c>0,④正确.
故选B.
点评 本题考查了二次函数图象与系数的关系,根据二次函数图象以及顶点坐标找出a、b、c之间的关系是解题的关键.

练习册系列答案
相关题目
2.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
19.当a,b满足 _______的时候,-|a-b|+7有最 _______(填大或小)值为 _______.( )
| A. | a=b,大,7 | B. | a=b,小,7 | C. | a=-b,大,7 | D. | a=-b,小,7 |
6.下列各式从左到右的变形中,是因式分解的为( )
| A. | x(a-b)=ax-bx | B. | $\frac{1}{{x}^{2}}$-1=($\frac{1}{x}$+1)($\frac{1}{x}$-1) | ||
| C. | x2-1=(x+1)(x-1) | D. | x2-1+y2=(x-1)(x+1)+y2 |
16. 如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
 如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )| A. | 3:1 | B. | 2:1 | C. | 5:2 | D. | 3:2 |
3.下列说法正确的是( )
①正整数和负整数统称为整数.
②-0.5既是分数,也是负数.
③0只表示没有.
④正数和负数统称为有理数.
⑤一个数不是正数就是负数.
⑥既不是正数也不是整数的有理数是负分数.
①正整数和负整数统称为整数.
②-0.5既是分数,也是负数.
③0只表示没有.
④正数和负数统称为有理数.
⑤一个数不是正数就是负数.
⑥既不是正数也不是整数的有理数是负分数.
| A. | ②⑥ | B. | ①②⑥ | C. | ④⑤⑥ | D. | ①⑤ |
1.现有两根木棒,它们的长分别是20cm和30cm.若要订一个三角架,则下列四根木棒的长度应选( )
| A. | 10 cm | B. | 30 cm | C. | 50 cm | D. | 70 cm |
 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.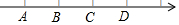 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别为整数a、b、c、d,且d-2a=4,则数轴的原点应是( )
如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别为整数a、b、c、d,且d-2a=4,则数轴的原点应是( )